zuloogator.blogg.se - Hanoi towers function

Hanoi towers function code#
Hanoi towers function series#

A psychological question on the side: Which size of towers can you move just by looking at the picture and for which size do you need to formalize `Divide` and `Build`? Or do you use another way of solving the puzzle? Does your method scale to even larger sizes? Can you write down an algorithm (in pseudocode) that works for any size of towers? (Ignore questions of efficiency for now, we will come back to this.) : Referring back to the note on [Recursion as a Problem Solving can you say what your methods for `Divide` and `Build` are? Write them down in English. **Activity:** Try to describe your algorithm.

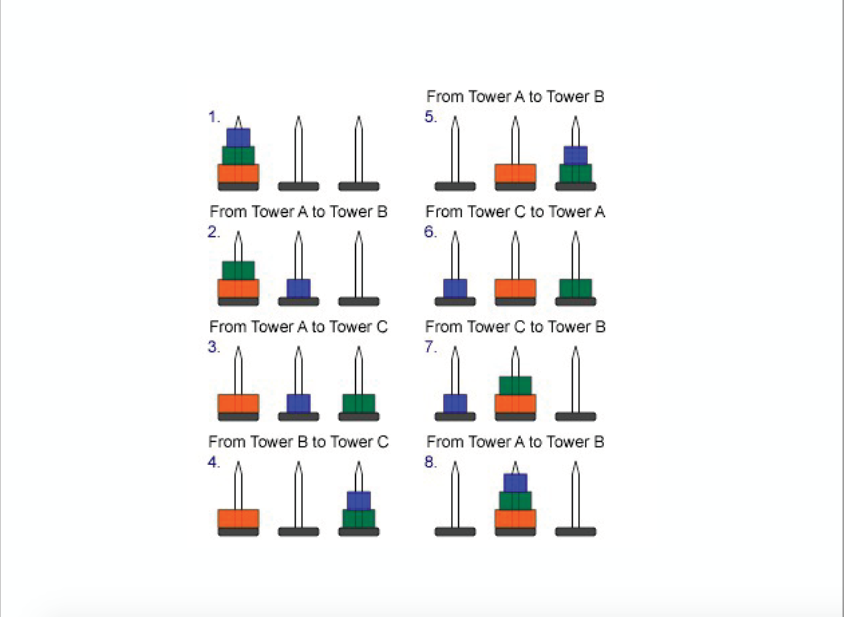
If you feel confident solving the puzzle with 5 or 6 disks, you may have found an algorithm which works for any number `n` of disks. **Activity:** How does it work for 4 disks? What is the biggest number of disks you can do? For size `n=3`, where do you have to place the top disk in the first move? There is only one correct answer. So, the expression for the N discs will become, Moves N = (2 * Moves N-1) + 1 = 2 N - 1. The number of moves almost doubles every time you insert another disk in the stack.

Hanoi towers function series#

For N = 3, the minimum number of moves required to shift from tower A to tower B is 7.Ĭan you observe some pattern or series from the above points?.

For N = 2, the minimum number of moves required to shift from tower A to tower B is 3.

For N = 1, the minimum number of moves required to shift from tower A to tower B is 1.

We can observe the following things from the above discussion: Let us now analyze the minimum number of moves required to shift all discs from tower A to tower B. TowerofHanoi(N - 1, inter, source, dest)

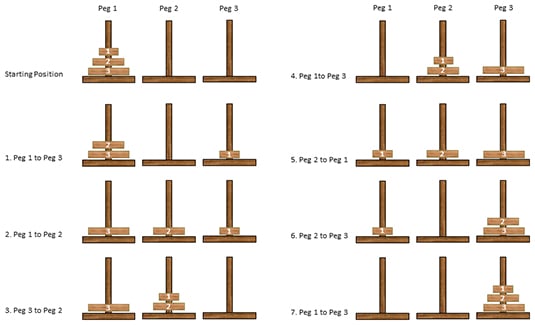
Moving N - 1 discs from tower C to tower B. Moving Nth disc from tower A to tower B.Ĭout<< "\t\tMove disc " << N << " from " << source <<" to "<< dest <<"\n" TowerofHanoi(N - 1, source, dest, inter) Moving N - 1 discs from tower A to tower C. void towerOfHanoi(int N, char source, char inter, char dest)Ĭout<< "\t\tMove Disc 1 from " << source << " to " << dest << "\n"

Hanoi towers function code#

Now again, recursively call the function’ towerOfHanoi()’ for N – 1 discs to move them from ‘inter’ to ‘dest.’īelow is the code snippet for the same approach for your reference.

Move the Nth disc from ‘source’ to ‘dest.’.

Else recursively call the function’ towerOfHanoi()’ for N – 1 discs to move them from ‘source’ to ‘inter.’.

Design a base Case for the solution as if ‘discs’ = 1, then move it from ‘source’ to ‘dest.’.

Create a function, let’s say towerOfHanoi() with integer variable ‘N’ representing the number of discs, three-character variables, say ‘source,’ ‘dest’ and ‘inter’ representing source, destination, and intermediate positions.

Now recursively move ‘N – 1’ discs from tower C to tower B.Īfter going through the discussion on the Algorithm above, you can try to write the recursive code by following the below-mentioned steps:.

Move the ‘Nth’ disc from tower A to tower B.Recursively, move top’ N – 1′ discs from tower A to tower C.Now let us derive the general solution for the ‘N’ number of discs. We can see that 7 moves will be required to shift 3 Discs from tower A to tower B with the help of an intermediary tower C.